Turns out ChatGPT can learn high level arithmetic concepts through Q&A with the user.
Initially, it factored 3136 into primes incorectly. And it mistakely thought a^m * b^n = (a * b)^(m * n).
After prompting, it figured out the correct answers.





Q: Factor 3136 into primes
3136 can be factored into the prime numbers 2, 2, 2, 2, 2, 3, 3, 3 as follows:
3136 = 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3 = 2^5 * 3^3
[…]
Q: What is 2^5 * 3^3?
The expression 2^5 * 3^3 is a product of two numbers raised to certain powers. In general, if a and b are numbers and m and n are positive integers, then a^m * b^n is equal to (a * b)^(m * n)
Therefore, 2^5 * 3^3 is equal to (2 * 3)^(5 + 3), which is equal to 6^8.
Thus, the value of 2^5 * 3^3 is 6^8, or 2985984.
Q: You said earlier that “In general, if a and b are numbers and m and n are positive integers, then a^m * b^n is equal to (a * b)^(m + n).” What happens when m=1 and n=2?
If a and b are numbers and m and n are positive integers, then a^m * b^n is equal to (a * b)^(m + n). So, if m=1 and n=2, then a^1 * b^2 would be equal to (a * b)^(1 + 2), or (a * b)^3.
Q: But that’s not true! Take for example a=1, b=2!
Yes, you are correct. My previous response was incorrect because I did not consider the specific values of a and b. If a=1 and b=2, then a^1 * b^2 would be equal to 1 * 2^2, or 4. This is not equal to (1 * 2)^3, which would be equal to 8.
Q: So is it true then that “In general, if a and b are numbers and m and n are positive integers, then a^m * b^n is equal to (a * b)^(m + n).”?
No, my previous statement is not always true. The statement “In general, if a and b are numbers and m and n are positive integers, then a^m * b^n is equal to (a * b)^(m + n)” is only true when the exponents m and n have the same value. For example, if m=2 and n=2, then a^2 * b^2 would be equal to (a * b)^(2 + 2), or (a * b)^4. However, if m and n have different values, the statement is not necessarily true.
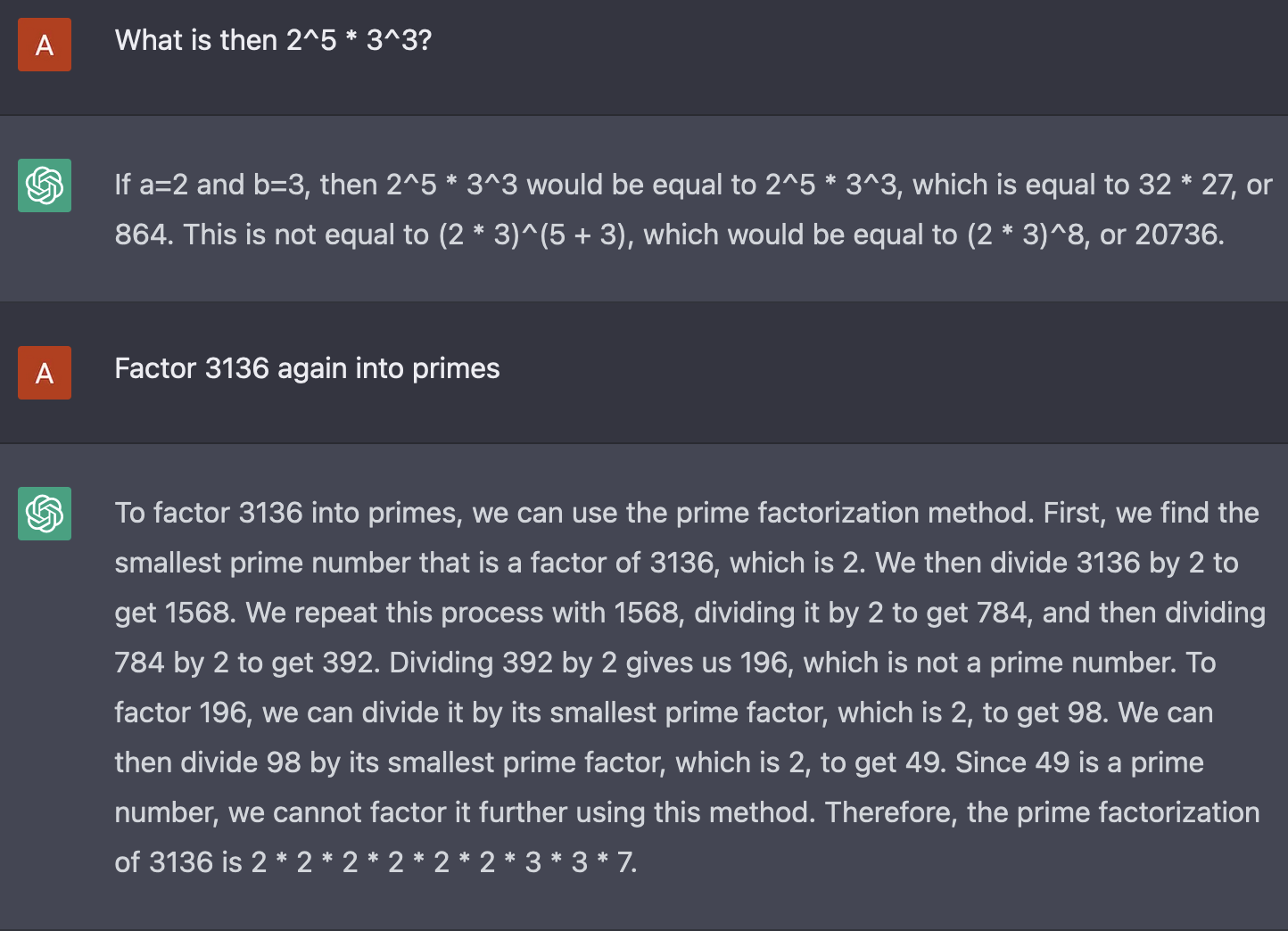
Q: What is then 2^5 * 3^3?
If a=2 and b=3, then 2^5 * 3^3 would be equal to 2^5 * 3^3, which is equal to 32 * 27, or 864. This is not equal to (2 * 3)^(5 + 3), which would be equal to (2 * 3)^8, or 20736.
Q: Factor 3136 again into primes
To factor 3136 into primes, we can use the prime factorization method. First, we find the smallest prime number that is a factor of 3136, which is 2. We then divide 3136 by 2 to get 1568. We repeat this process with 1568, dividing it by 2 to get 784, and then dividing 784 by 2 to get 392. Dividing 392 by 2 gives us 196, which is not a prime number. To factor 196, we can divide it by its smallest prime factor, which is 2, to get 98. We can then divide 98 by its smallest prime factor, which is 2, to get 49. Since 49 is a prime number, we cannot factor it further using this method. Therefore, the prime factorization of 3136 is 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 7.
Q: You said 49 is a prime number. Can you double check that?
Yes, you are correct. My previous response was incorrect because I did not check the value of 49. 49 is not a prime number, it is a composite number. This means it can be factored into smaller positive integers. The prime factorization of 49 is 7 * 7. I apologize for the mistake.
Q: Factor 3136 again into primes
To factor 3136 into primes, we can use the prime factorization method. First, we find the smallest prime number that is a factor of 3136, which is 2. We then divide 3136 by 2 to get 1568. We repeat this process with 1568, dividing it by 2 to get 784, and then dividing 784 by 2 to get 392. Dividing 392 by 2 gives us 196, which is not a prime number. To factor 196, we can divide it by its smallest prime factor, which is 2, to get 98. We can then divide 98 by its smallest prime factor, which is 2, to get 49. Since 49 is not a prime number, we need to factor it further. The prime factorization of 49 is 7 * 7, so we can write 49 as 7 * 7. Substituting this back into our expression for 3136, we have 3136 = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 7 * 7. This is the prime factorization of 3136.
Q: How did you get the 3 * 3 factors in? Double check that.
In my previous response, I mistakenly wrote that the prime factorization of 3136 was 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 7. This is not correct, because 3136 is not divisible by 3. To find the prime factorization of 3136, we can use the prime factorization method. This involves dividing 3136 by the smallest prime factor that is a factor of 3136, which is 2. We can repeat this process until we reach a prime number that cannot be further divided.
To do this, we start by dividing 3136 by 2 to get 1568. We then divide 1568 by 2 to get 784. Dividing 784 by 2 gives us 392, and dividing 392 by 2 gives us 196. Since 196 is not a prime number, we need to divide it further. The smallest prime factor of 196 is 2, so we divide 196 by 2 to get 98. Dividing 98 by 2 gives us 49, which is not a prime number. To factor 49, we can divide it by its smallest prime factor, which is 7. Dividing 49 by 7 gives us 7, which is a prime number. Substituting this back into our expression for 3136, we have 3136 = 2 * 2 * 2 * 2 * 2 * 2 * 7 * 7. This is the prime factorization of 3136.
I apologize for any confusion my previous response may have caused. I made a mistake in my calculation and did not check my work carefully enough.