Notes on Deep Learning Course at CDS

05L - Joint embedding method and latent variable energy based models (LV-EBMs), slides

  • Energy based models (EBM) vs Discriminative models
    • Energy \(F(x, y)\), where \(x\) is observed variable, and we’d like to predict variable \(y\).
    • Find \(\check(x)=argmin_y F(x, y)\) (energy is minimized)
    • Choice of energy function does not matter if minimum is achieved for same value \(y\). For example, if we add a constant to \(F\), the minimum does not change.
    • Can compute if \(y\) is discrete, or if there is a dynamic-programming-style way to compute \(y\)
    • Energy \(F(x, y)\) computed during training
    • If \(F\) is a smooth function of \(y\), can use gradient descent during inference to compute \(\check{y}\)

  • Factor Graphs
  • Conditional EBM: \(F(x, y)\) has conditional variable \(x\)
  • Unconditional EBM: \(F(y)\). Here, \(x\) does not exist.
    • PCA
    • k-means clustering
    • Any unsupervised algorithm can be cast as unconditional EBM
  • Both \(x\), \(y\) are inputs to model \(F\).
  • Connection to probabilistic models
    • Probabilistic models are special case of EBM
    • Energies are like un-normalized negative log probabilities
  • Why use EBM instead of probabilistic models?
    • EBM gives more flexibility in
      • Choice of scoring function
      • Choice of objective function for learning
  • From energy to probability: Gibbs-Boltzmann distribution
\[\begin{align*} P(y \vert x) = \frac{e^{-\beta F(x, y)}}{\int_{y'} e^{-\beta F(x, y')}} \end{align*}\]
  • Softmax is an instance of the Gibbs-Boltzmann distribution
  • You pick \(\beta\), it is arbitrary
    • For physicists, this constant is aking to temperature.
  • The exponential makes numbers positive. Gives high values to low energy (which is what you want - likely configurations have low energy)
  • Denominator is normalization factor
  • LeCun does not say it - but \(P(y \vert x)\) can be seen as number of configurations with energy \(F(x, y)\) (but normalized)
  • Energy function is like a cost we want to minimize
  • Inference becomes optimization problem to find \(y\)

EBM architectures:

  • Joint embeddings
  • Variational models

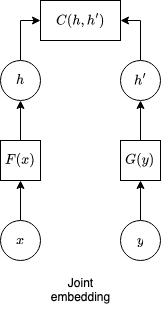
  • In joint embedding, inputs can be both images.
    • \(G(y)\) can be invariant to changes of luminosity, for example.
    • This means we get multiple values of \(y\) with same \(h'\).
    • Specific case: siamese nets, when \(F,G\) are identical

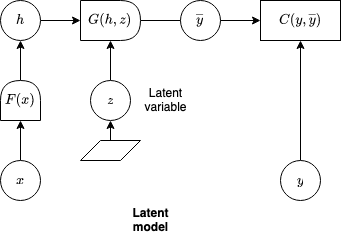
  • General setup for latent variable: \(E(x, y, z)\) where \(z\) latent
    • Find \(argmin_y min_z E(x, y, z)\)
    • Can eliminate z replacing \(E\) with free energy: \(F_\beta(x, y) = - \frac{1}{\beta} \log \int_z e^{- \beta E(x, y, z)} dz\)
    • When \(\beta=\infty\), this becomes \(F_\infty(x, y) = min_z E(x, y, z)\)
    • Called free energy by physicists
  • We use energy models when marginal probability in Gibbs-Boltzmann distribution is intractable
  • We diminish our ambitions here! Use energy as fundamental underlying object.
  • Where does energy come from?
\[\begin{align*} P(y, z \vert x) = \frac{e^{- \beta E(x, y, z)}}{\int_{y, z}e^{- \beta E(x, y, z)}dydz} \end{align*}\] \[\begin{align*} P(y \vert x) &= \int_z P(y, z \vert x) \\ &= \frac{\int_z e^{- \beta E(x, y, z)}dz}{\int_{y, z}e^{- \beta E(x, y, z)}dydz} \\ &= \frac{e^{-\beta \left[ -\frac{1}{\beta}\ln \int_z e^{- \beta E(x, y, z)}dz\right]}} {\int_y e^{-\beta \left[ -\frac{1}{\beta}\ln \int_{z}e^{- \beta E(x, y, z)}dz\right]}dy} \\ &= \frac{e^{-\beta F_\beta(x, y)}} {\int_y e^{-\beta F_\beta(x, y)}dy} \end{align*}\]
  • That’s where the free energy formula comes from.
  • K-means as energy model
  • Limiting the capacity of the latent variable \(z\)
    • k-means solves this by setting \(z\) to be discrete
  • Training EBM
    • Give it an architecture/energy function \(F(x, y)\)
    • For each datapoint \((x[i], y[i])\), tweak \(F\) so energy is as small as possible
    • Then, we need the energy of other \((x[i], y')\) to be as large as possible
    • Keep \(F\) smoothxs
    • Two methods:
      • Contrastive method: push down \(F(x[i], y[i])\), push up other points \(F(x[i], y')\)
      • Regularized/Architectural methods: build \(F(x, y)\) so that volume of low energy regions is minimized through regularization
    • Contrastive
      • C1: push down energy of data points, push up everything else
        • Max likelihood
      • C2: push down energy of data points, push up chosen locations
        • Max likelihood with MC/MMC/HMC
        • Contrastive divergence
        • Metric learning/Siamese nets
        • Ratio matching
        • Noise contrastive estimation
        • Min probability flow
        • Adversarial generation/GAM
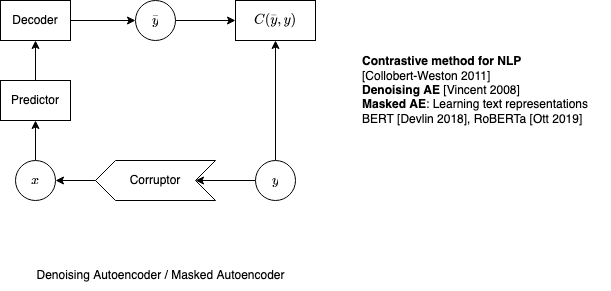
      • C3: train a function that maps points off the data manifold to points on the data manifold:
        • Denoising autoencoder
        • Masked autoencoder (e.g. BERT)
    • Regularized/Architectural
      • A1: build the machine so the volume of low energy space is bounded:
        • PCA
        • K-means
        • Gaussian mixture model
        • Square ICA
        • Normalizing flows
      • A2: use a regularization term that measures the volume of space that has low energy:
        • Sparse coding
        • Sparse auto-encoder
        • LISTA
        • Variational auto-encoders
        • Discretization/VQ/VQVAE
      • A3: \(F(x, y)=C(y, G(x, y))\), make \(G(x, y)\) as “constant” as possible with respect to \(y\)
        • Contracting auto-encoder
        • Saturating auto-encoder
      • A4: minimize the gradient and maximize the curvature around data points: score matching

Why is max likelihood a contrastive method: we want to pick weights \(w\) to maximize

\[\begin{align*} p_w(y \vert x) &= \frac{e^{- \beta F_w(x, y)}}{\int_{y'}e^{- \beta F_w(x, y')}dy'} \\ \end{align*}\]

Taking logs, this is same as to minimize:

\[\begin{align*} \mathcal{L}(x, y, w) &= F_w(x, y) + \frac{1}{\beta} \log \int_{y'}e^{- \beta F_w(x, y')}dy' \end{align*}\]

Taking gradient w/ respect to \(w\):

\[\begin{align*} \frac{\partial}{\partial w}\mathcal{L}(x, y, w) &= \frac{\partial}{\partial w} F_w(x, y) + \frac{1}{\beta} \frac{\partial}{\partial w} \log \int_{y'}e^{- \beta F_w(x, y')}dy'\\ &= \frac{\partial}{\partial w} F_w(x, y) + \frac{1}{\beta} \frac{\frac{\partial}{\partial w} \int_{y'}e^{- \beta F_w(x, y')}dy'}{\int_{y'}e^{- \beta F_w(x, y')}dy'} \\ &= \frac{\partial}{\partial w} F_w(x, y) + \frac{1}{\beta} \frac{ \int_{y'}\frac{\partial}{\partial w}e^{- \beta F_w(x, y')}dy'}{\int_{y'}e^{- \beta F_w(x, y')}dy'} \\ &= \frac{\partial}{\partial w} F_w(x, y) - \frac{ \int_{y'}e^{- \beta F_w(x, y')}\frac{\partial}{\partial w}F_w(x, y')dy'}{\int_{y'}e^{- \beta F_w(x, y')}dy'} \\ &= \frac{\partial}{\partial w} F_w(x, y) - \int_{y'} p(y' \vert x) \frac{\partial}{\partial w}F_w(x, y')dy' \\ \end{align*}\]

We can backpropagate through the left term.

Under the integral, if \(y'\) has high energy, \(p(y' \vert x)\) is low, and \(\frac{\partial}{\partial w}F_w(x, y')\) is not pushed up very much. If \(y'\) has low energy, \(p(y' \vert x)\) is high, \(\frac{\partial}{\partial w}F_w(x, y')\) is pushed up.

Issues

  • Integral is most time intractable
  • You can discretize the integral, but you still have to sum over all y. If \(y\) is in a discrete space, \(F\) is actually softmax.
  • If the space is large, even discretized, it is too large.
  • We can instead pick a single sample \(y'\).
  • Back during WW2, during the Manhattan project, physicists invented the Monte-Carlo method, for a distribution that has only the energy, and not the distribution.
  • MC/MCMC/HMC/CD: Draw a sample \(\hat{y}\) from \(F_w(y \vert x))\), and replace the integral with that sample.
  • If you draw sufficiently many samples, get good approximation:
\[\begin{align*} \frac{\partial}{\partial w}\mathcal{L}(x, y, w) &\approx \frac{\partial}{\partial w} F_w(x, y) - \frac{\partial}{\partial w}F_w(x, \hat{y}) \end{align*}\]
  • If \(y\) space is very large, you will need a lot of samples
  • Boltzmann machines, restricted Boltzmann machines - this is how they are trained
  • MC, or MCMC methods for probabilistic graphical models - this is how they are trained
  • \(\beta\) is to some extent arbitrary. You can pick value 1. For example, if you use softmax, you can rescale the previous layer so that \(\beta\) in the softmax becomes 1.

Gradient descent:

\[\begin{align*} w & \leftarrow w - \eta \frac{\partial}{\partial w}\mathcal{L}(x, y, w) \\ &= w - \eta \frac{\partial}{\partial w} F_w(x, y) + \eta \frac{\partial}{\partial w}F_w(x, \hat{y}) \end{align*}\]
  • First \(\eta\) term pushes down on the energy of samples
  • Second \(\eta\) term pushes up on the energy of low-energy samples

Problems with this method:

  • Large space of \(y\) requires many samples
  • This method wants to push the bad \(y\)s to infinite energy
    • Tell this to a statistician, they will murder you on the spot! It says the probabilistic approach does not function.
    • Baesian statisticians have invented all sorts of things to prevent this from happening
    • The loss must be regularized to keep the energy smooth
    • But those are hacks, and you might as well use good hacks!

Instead of insisting that the energy is a log probability - just ensure that the energy of good points is lower than that of bad points.

Example cost functions:

  • Simple: Bromley 1993:
\[\begin{align*} \mathcal{L}(x, y, \hat{y}, w) = [F_w(x, y)]^+ + [m(y, \hat{y}) - F_w(x, \hat{y})]^+ \end{align*}\]
  • Pick non-matching \(\hat{y}\) by some method
  • Push up \(F_w(x, \hat{y})\) but not more than \(m(y, \hat{y})\)

  • \([]^+\) is ReLU function

  • Hinge pair loss: Altun 2003, Ranking loss: Weston 2010: I don’t care if \(F_w(x, y)\) is close to 0, I just want it less than \(F_w(x, \hat{y})\)
\[\begin{align*} \mathcal{L}(x, y, \hat{y}, w) = [F_w(x, y) - F_w(x, \hat{y}) + [m(y, \hat{y}) ]^+ \end{align*}\]
  • Square-square loss: Chopra CVPR 2005, Hadsell CVPR 2006:
    • Square ensures convexity, which helps convergence
\[\begin{align*} \mathcal{L}(x, y, \hat{y}, w) = ([F_w(x, y)]^+)^2 + ([m(y, \hat{y}) - F_w(x, \hat{y})]^+)^2 \end{align*}\]
  • All possible outputs: Hinge loss
\[\begin{align*} \mathcal{L}(x, y, \hat{y}, w) = \sum_{\hat{y} \in \mathcal{Y}}[F_w(x, y)]^+ + [m(y, \hat{y}) - F_w(x, \hat{y})]^+ \end{align*}\]
  • Group losses: Neighborhood Component Analysis, Noise Contrastive Estimation (implicit infinite margin): Goldberger 2005, Gutmann 2010, …, Misra 2019, Chen 2020
\[\begin{align*} \mathcal{L}(x, y, \hat{y}_1, ... \hat{y}_{p^-}, w) = \frac{e^{-F_w(x, y)}}{e^{-F_w(x, y)}+\sum_{i=1, ..., p^-} e^{-F_w(x, y_i)}} \end{align*}\]
  • Contrastive joint embeddings

  • Denoising or mask autoencoder

06L - Latent variable EBMs for structured prediction slides

  • Recap of last lecture
  • Group losses: Neighborhood Component Analysis, Noise Contrastive Estimation (implicit infinite margin): Goldberger 2005, Gutmann 2010, …, Misra 2019, Chen 2020
\[\begin{align*} \mathcal{L}(x, y, \hat{y}_1, ... \hat{y}_{p^-}, w) = \frac{e^{-F_w(x, y)}}{e^{-F_w(x, y)}+\sum_{i=1, ..., p^-} e^{-F_w(x, y_i)}} \end{align*}\]
  • Used with a batch that contains \(y\) and all \(\hat{y}_i\)
  • If a single \(\hat{y}_i\) has low energy, and all other \(\hat{y}_j\) have high energy, gradient of weights will be pushed hard around \(\hat{y}_i\) but not other \(\hat{y}_j\)
  • SSL for speech recognition: Wav2Vec2.0: Baevski et al. NeurIPS 2020, Xu et al. ArXiv:2010.11430, Github: PyTorch/fairseq
    • Raw audio → ConvNet → Transformer
    • Create foundational model trained on 960h speech with contrasting embedding of speech
    • Transfer learning for 10m, 1h or 100h of labeled speech
  • XLSR: multilingual speech recognition: Conneau arXiv:2006.13979
    • Raw audio → ConvNet → Transformer
  • GANs as contrastive energy models
    • References
    • Need to figure out how to pick samples whose energy to push up
    • In GANs, push samples that have low energy, but are not part of training
    • Will train a NN \(Gen(z)\) to generate the bad samples

  • Pick \(y, \hat{y}\). Backpropagate through \(Critic(y)\) to increase \(C(\hat{y},y)\).
  • Backpropagate \(\hat{y}\) through both nets, but freeze \(Critic()\) and change weights only in \(Gen(z)\). This reduces energy of \(\hat{y}\)
  • \(Gen(z)\) is trained to produce the negative samples
  • Drop the critic to generate images
  • GANs did not work very well originally
  • Energy-Based GAN [Zhao 2016], Wasserstein GAN [Arjovsky 2017],… improved GANs by making energy function smooth. If you’re not careful, energy surface becomes canyon. You have to regularize the critic, and that’s essentially what Wasserstein GANs do.
  • Optimization is finding a Nash equilibrium (a saddle point). With gradient descent, hard to find - get mode collapse, when critic does not give any useful gradients (and generator keeps producing same output)
  • With original GANs, if you train long enough, you have collapse
  • Wasserstein GANs are a way to deal with this. Though even with Wasserstein GANs, if you train long enough, you get mode collapse.
  • Attempts to use critic as base for transfer learing have failed. Only generator can be used to generate data.

Non-Contrastive Methods for Joint Embedding

  • Eliminates hard negative mining
  • Siamese nets with slightly different weights
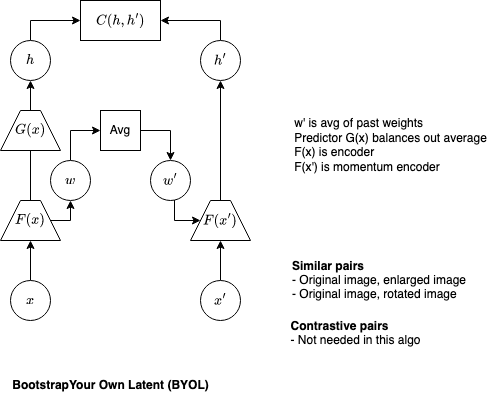
    • Bootstrap Your Own Latent (BYOL), J-B Grill et al (2020), Deep Mind
      • Use siamese networks
      • But right network uses average of past weights of left network
      • Idea is from MOCO - momentum embedded in these weights
        • But MOCO largely outdated in last year or two

  • SwAV, Caron arXiv:2006.09882
  • DeepCluster, Caron arXiv:1807.05520
  • SimSiam: [Exploring Simple Siamese Representations)(https://arxiv.org/pdf/2011.10566.pdf), Chen et al, 2020
  • Barlow Twins, Zbontar et al. ArXiv:2103.03230
  • Use SwAV as foundational model for SEER, Goyal et al. ArXiv:2103.01988

Latent Variable Models in Practice

  • Use latent variable when you can have multiple outputs for same input - or if output has some structure
  • As you vary latent variable, prediction varies over all plausible outputs that correspond to input
  • DETR: End-to-End Object Detection with Transformers, Carion et al (2020)
    • ConvNet → Transformer
      • ConvNet invariant to translation
      • Transformer invariant to permutation (if input is permuted, so is output)
      • Can do semantic segmentation with it

07L - PCA, AE, K-means, Gaussian mixture model, sparse coding, and intuitive VAE, slides

  • Recap
  • Faces have 50 degrees of freedom - suggest dimension of latent space
  • Architectural models limit the dimension of the latent space
  • PCA is an autoencoder with projection encoder, linear decoder.
    • Energy: \(F_w(y) = \vert \vert y - Dec(Enc(y)) \vert \vert ^2 = \vert \vert y - w^Ty \vert \vert ^2\)
    • Loss: \(L(y,w)=F_w(y)\)
    • If using linear encoder (instead of projection), get PCA latent representation but up to affine transform (rotation+translation) in the latent space
  • Auto-encoder
    • Energy: \(F_w(y) = \vert \vert y - Dec(Enc(y)) \vert \vert ^2\)
    • Loss: \(L(y,w)=F_w(y)\)
  • k-Means
    • Discrete latent-variable model with linear decoder
    • Energy: \(E(y,z) = \vert \vert y - Dec(z) \vert \vert ^2 = \vert \vert y - wz \vert \vert ^2\)
    • Free Energy: \(F(y) = \underset{z \in Z}{\min} E(y,z)\)
    • Loss: \(L(y,w)=F_w(y)\)
      • Latent vector \(z\) is constrained to be 1-hot vector \([..., 0, 1, 0, ...]\)
      • \(wz\) selects one colum of \(w\)
      • Free energy minimized around colums of \(w\)
    • Algorithm:
      • We’re given set of samples \(y\)
      • Pick \(w\)
      • Compute loss \(L(y, w)\) on set of samples \(y\)
      • Change \(w\) in the direction of minimizing loss, either using gradient descent, or, in this case, direct computation.
    • You don’t need contrastive learning, you don’t need to push on anything, b/c volume of latent variable is constrained - in this case, actually discrete.
    • Don’t necessarily need a linear decoder for this to work.
  • Gaussian Mixture Model
    • Similar to k-means with soft marginalization over latent
      • k-means use quadratic balls
      • Gaussian mixture allows balls to take any shape within quadratic form - allow them to be elongated in some directions but not others
      • Gaussian mixture can be “elongated along the data”. Thus, it can model the data with fewer samples.
    • Energy: \(E(y, z) = (y-wz)^T (Mz) (y-wz)\)
      • Here \((Mz)_{ij} = \sum_{k} M_{kij}z_k\)
    • Free Energy: \(F(y) = - \frac{1}{\beta} \log \sum_{z \in Z} e^{\beta E(y,z)}\) (but LeCun says he’s missing a term - the mixture coefficients, that compute a weighted sum of the energies)
    • Loss: \(L(y,w) = F_w(y)\) with normalization constraint on \(M\)
      • Latent vector \(z\) is constrained to be 1-hot vector \([..., 0, 1, 0, ...]\)
      • But marginalization makes it soft
      • \(wz\) selects column of \(w\)
      • Columns of \(w\) are centers of Gaussians
      • Then, compute a distance, but distance is warped by a certain tensor \(M\), symmetric positive semi-definite, which is actually the universe covariance matrix of the Gaussians
      • \(z\) being one-hot vector, it selects slice of matrix \(M\).
        • Think of \(M\) as several slices of covariance matrices. \(z\) selects one of them.
      • \(z\) selects the mean, then selects the covariance matrix
      • Overall energy of Mixture is marginalization over \(z\).
      • We’re not minimizing anymore, we’re marginalizing.
      • You can set \(\beta\) to 1, it does not matter. Make a choice.
    • How do you train it?
      • Use EM (Expectation Maximization)
      • You could use gradient descent, does not work very well. Gets you stuck to a local minimum.
      • Will not explain EM.
    • It’s an architectural model because you constrain the \(M\) matrix
    • You have to guarantee that the covariance matrix has constant determinant.
  • Regularized Energy Based Models
    • Instead of constraining the volume of the latent variable, have a regularization term that will constrain it
    • Energy: \(E(x, y, z) = C(y, Dec(Pred(x),z)) + \lambda R(z)\)
    • Examples of \(R(z)\):
      • Effective dimension
      • Quantization / discretization. Bayesians do this with Dirichlet allocation. Called LDA - Latent Dirichlet Analysis. Dirichlet can be pronounced in French, but he was German actually.
      • L0 norm (# of non-zero components of a vector). Find \(z\) that I could use, such that \(z\) has minimum non-zero components. Will pay a price for each non-zero component. Problem: not a differential criterion. Hard to optimize. There are approximate methods, one is projection pursuit: find a component where you can project, to minimize cost. Then, find a 2nd component you can project, to still minimize cost, and so on.
      • L1 norm with decoder normalization. Compute the sum of the absolute values of the components of \(z\). Minimize that. Called sparse coding. Compared to L0, it is a convex method. And it’s an approximation of L0 - it produces a sparse vector, eventually. L1 norm method is called sparse coding. Decoding is called sparse decoding.
      • Maximize lateral inhibition / competition.
      • Add noise to z while limiting its L2 norm (VAE)
        • I forbid \(z\) to go outside a given sphere, but I add noise to \(z\) to make it a fuzzy value. LeCun applauds while speaking, to make the point that you have to focus on content while he adds noise.
  • References

08L – Self-supervised learning and variational inference , slides

  • Review of GANs as constrastive energy-based models (EBMs)